图灵的秘密-随笔
初衷
读完《编码:隐匿在计算机软硬件背后的语言》的时候,我就深深折服于Charles Petzold大叔化繁为简的能力和穿针引线的技巧。几年前听说他又出了本有关图灵的新书《图灵的秘密:他的生平、思想及论文解读》,第一时间就找来原版拜读,可惜英文水平有限,囫囵吞枣之后感觉意犹未尽。
幸好最近得闲,又找来中文版细细品味。不禁感叹,酒香不怕巷子深,图灵还是你祖师爷。
遂留下此文,方便日后再品。
整理
图灵论文的脉络
首先需要强调的是:图灵这篇论文原本是用来证明”谓词逻辑没有通用判定过程”这个命题的(回应希尔伯特的假设),图灵机(确切的说是通用图灵机)只是这个证明的副产品。仅仅是这个副产品,就已经成为后世膜拜的经典,天才可见一斑。
根据Charles Petzold大叔的解读,我将论文中的一些概念加以整理,梳理出大体脉络(图1),欢迎大家指正:
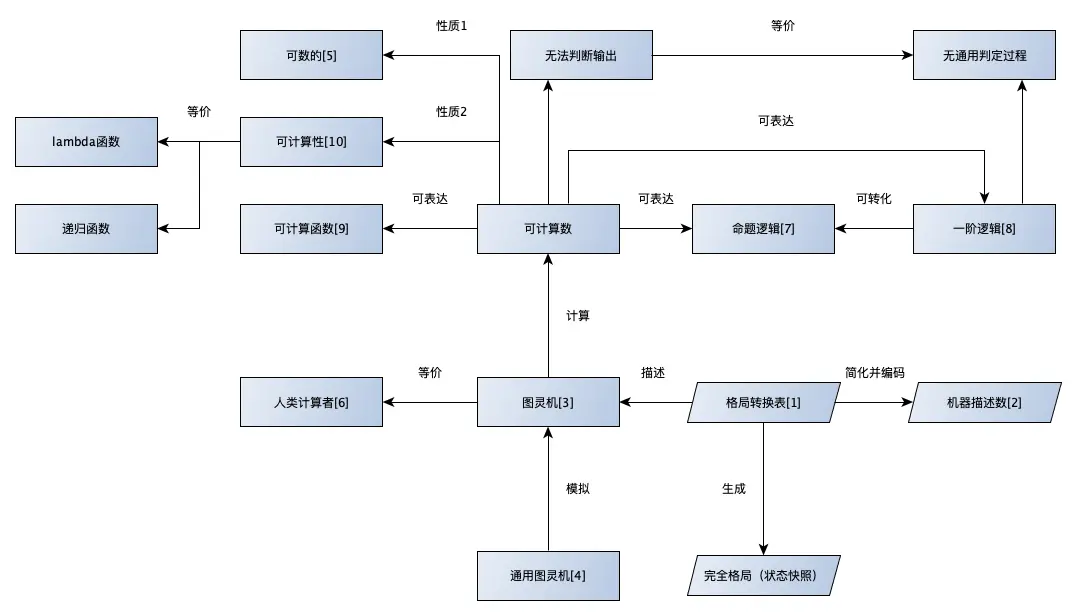
图中的关键点说明:
- 格局转换表(m-configuration-table):包含了图灵机进行状态切换时所执行的指令(打印/擦除/移动)。本质上,这张表描述了图灵机如何进行计算,即它是一种算法。
- 机器描述数(Desc Number):将每一个格局最简化并编码后连接而成的整数。它拥有如下特点:
- 每一个机器描述数对应一个可计算数
- 由于可以将格局按照不同次序进行排列得到新的整数,所以一个可计算数可能对应多个机器描述数
- 不是每一个整数都符合机器描述数的定义,机器描述数是稀疏的
- 机器描述数是一个有限位数的整数,却可以用来表达一个拥有无限位数的实数(例如PI)
- 图灵机(Turing Machine):格局转换表完整描述了可能遇到的所有状态,并通过在纸带上打印0,1进行计算的机器。图灵概念中一个好的图灵机(非循环的)必须不断输出0或者1,永不停止。
- 通用图灵机(UTM):一个图灵机,输入特定的机器描述数即可模拟运行该机器,并得到被模拟机器的输出。
- 可数的:可计算数是可数的,对应自然数的无穷。所有0和1构成的无限序列是不可数的,对应实数的无穷。
- 等价的意义:为了说明图灵机做不了的事人类也做不了(有可能是错的,如果人类的大脑不仅仅遵循机械计算的原则)。
- 命题逻辑:通过将命题逻辑中的变量按照真假取值编码(0为假,1为真),可以用一个有限的数列表达一个命题逻辑的取值(每一位对应真值表中的一行)。
- 一阶逻辑:通过将论域(自然数集合)中的个体(每个自然数)依次代入,可以将一阶逻辑转化为一个个命题,并判断真假。又因为谓词是逻辑的抽象,所有谓词都可以置换到自然数论域中。因此一阶逻辑可以用可计算数表达。
- 可计算函数:通过将y=f(n)定义为第n个连续的0之间的1的个数,可以将可计算函数和可计算数相关联。
- 可计算性:图灵机的计算能力等价lambda函数和一般递归函数。
经过整理之后得到的图灵的论证逻辑:
- 定义图灵机并证明它的计算能力和人类计算者相同,图灵机输出的是可计算数。
- 可计算数有两条性质:
- 可数但无法有效枚举:由于对角线法一定能找到一个不在可计算数列表中的数(而寻找这个数的算法又是可以描述的),因此矛盾只能因为无法枚举所有可计算数而存在。等价于不存在判定一个DN描述的图灵机是否是非循环的通用过程(例如遇到判定算法自身的机器DN该过程就会无限循环)。
- 可计算数包含所有可以被计算的数。
- 图灵机有能力通过字符替换,从公理推出所有定理。因此图灵机输出的可计算数可以由一阶谓词定义。
- 构造一个谓词Un(DN)表达一个图灵机是否打印0,该谓词可证明等价于存在判断图灵机是否打印0的通用过程。因为后者不存在,所以一阶谓词的通用判定过程不存在。
论文的初衷
既然这篇论文是为了反驳”谓词逻辑没有通用判定过程”,这里有必要展开聊一下这个命题存在的背景和意义。
“是否存在通用算法来判定一阶谓词逻辑”是希尔伯特的”判定性问题”。其之所以著名是因为在当时”形式主义”崛起的背景下,希尔伯特相信所有的数学问题都可以用谓词逻辑来表达,并通过公理系统推理得到真假。如果存在判定一阶谓词逻辑的通用算法,推理本身就可以被机械的计算所代替。而通过计算,人们必然能够得到命题是真还是假,而不存在悖论的可能。由此为基石构筑的数学体系就是坚不可摧的。
既然图灵已经证明不存在这样的通用判定过程,那么计算和推理就依然存在本质区别。
计算和推理的过程中都存在变换和重写,本质区别究竟在哪里?有一种观点认为:
- 计算规范的一系列步骤一定会产生一个结果并结束(停机)。
- 推理进行的变换在命题成立时可以有效结束,但是如果命题不成立时会无限进行下去。
都是无穷造的孽。
对后人的影响
图灵机本是一种存在于思想中的理想化的机器。但是后人遵循这个指引实现的计算机却直接催生了第三次工业革命。
非循环机和循环机
图灵定义的机器需要不断的计算输出0或者1,因为可计算数的位数是无限的。这种机器被称为非循环机,相反由于找不到对应的格局而进入假死状态的机器被称为循环的(这两个概念定义往往令初次遇见的人感到费解)。
但是现实生活中人们解决问题时可以动用的资源往往是有限的:我们需要在有限时间内获得足够精度的解。因此解决问题之后可以自动停下来的机器才是符合人们期望的。
于是出现了有限自动机的概念,其在图灵机的基础上做了如下剪裁:
- 状态有限,分为开始状态和接纳状态
- 输入符号有限,读取完毕即结束(磁头只能朝一个方向移动)
- 根据输入符号和当前状态转换机器的状态,但不能输出字符
- 结束时如果处于接纳状态,则符号被接纳,否则被拒绝
而有限自动机是可以判定的。
通用图灵机
制造能够模拟其它机器运行的通用计算机是一个相当吸引人的目标。在图灵从理论上论证了通用机可行之后,由冯诺伊曼为代表的科学家们付之行动,真正从物理上构建出了这样的通用计算工具。
满足冯诺伊曼体系的计算机和图灵机之间存在如下关联:
| # | 图灵机 | 冯诺伊曼体系 |
|---|---|---|
| 1 | 格局表 | 由控制和计算单元负责执行的指令集 |
| 2 | 纸带 | 内存 |
| 3 | 读写头 | 对内存的读写 |
| 4 | 符号 | 数据 |
| 5 | 输入输出设备 |
其中输入输出设备是方便使用者与机器进行交互而增加的组件。
冯诺伊曼结构计算机的一大特征是把指令本身作为数据存储,相当于被模拟的图灵机的格局转换表,这被称为可编程性。
由此现实当中至少存在三个层次上的通用图灵机:
- 计算机硬件
机器指令集作为格局转换表的图灵机,运行被模拟程序对应的机器码。 - 虚拟机
类似Java/Python之类的程序语言定义了自己专有的指令集并实现了运行这些指令的虚拟机,在这些虚拟机上模拟运行对应的程序字节码。 - 编程语言
编程语言本身即可以描述算法,自身的语法即对应指令集。
这三个层次之间具有相等的描述算法的能力,称为图灵完备。它们相互之间通过编译进行转换。
随想
公理化思维和艺术作品
公理化思维是指从一组公理开始,通过推理演绎得到新知识的过程。公理作为知识构筑的基石,其不证自明的正确性成为一切的根本。
要是公理被推翻呢?不谈其在现实中发生会带来的灾难,这个构想本身就可以作为艺术作品的摇篮。
越来越多的艺术作品构筑于虚构的公理,平行宇宙,时间旅行,心灵感应已经是好莱坞电影和日本动画的家常便饭,也催生出无数脍炙人口,发人深省的佳作。
这里提出一种构思虚拟世界的方式:
- 假设一组公理(层次越基础越好)
- 将这组公理正交衍生出定理
- 将衍生出的定理之间正交衍生出更多定理,不断往复这个过程
把人(或者其他)放在这么一个虚拟世界中,像上帝一样观察它,记录它。
算法和通用图灵机
通用图灵机将算法视为数据,模拟执行算法。
在现实中,人们发现把设计的复杂度放在算法上,制造机制相对简单(指令集较小)的通用机带来的收益最大。而图灵机器描述数的构成也揭示了完成同一个目标,存在不同的算法。
因此,针对通用机和算法,存在不同的优化目标:
- 通用机
提升机器性能,主要指指令执行速度的提升(提升系统总线频率,减少数据传输的开销,提高CPU的频率等最终都服务于这一目的)。
在单核性能提升逐渐遇到瓶颈时,专向多核并发。 - 程序(算法)
优化算法的复杂度,减少完成目标所需执行的指令规模。
其它优化思路
机器意识
计算能否产生意识?这个问题是机器能否产生智能的核心问题。目前引入概率方法,机器已经在模式识别方面有了显著的突破。可是它依然没有自我的概念。
硬件指令集
图灵已经论证了所有图灵机的计算能力是相同的,即使是引入量子计算,提升的也是计算速度,并不能扩大计算的边界。
我们也知道,算法并不能完全替代推理,仍然存在不能用算法解决的问题。
那么,是否在硬件层面能找到和推理直接对应的更自然的模拟机制?或者将不确定性引入指令集?
软件(算法)
现实中我们设计算法有两层用意:
完成目标
通过分治/动态规划/贪心等方法系统的提出解决某个问题的计算过程。优化目标
内存从物理上对应数组结构,通过指针关联之后产生各种高级数据结构:- 1对1即链表
- 1对多即树
- 多对多即图
在高级数据结构之上可以设计对应的算法降低解决问题需要的计算规模。
因此内存的随机读取能力是数据结构依赖的基础。
存在更高级的数据结构吗?异或将指针这个基础机制进行变形?